当我们学习一个新的编程语言时,输出的第一句话一定是“Hallo World”;当我们学习一个新的深度学习框架时,跑的第一个数据集一定是MNIST。这是Tensorflow官方教程的原话。MNIST是一个简单的计算机图像数据集,它由一系列大小为28×28的手写数字图像以及它们的标记组成(如下图所示),可以算是最简单的数据集之一啦。
本次学习会使用两种不同的方法对MNIST进行训练:Softmax回归和卷积神经网络。它们分别会得到不同精确度的手写数字预测模型。
导入MNIST数据
MNIST数据集可以直接在它的官网上下载,也可以通过Tensorflow的教程文件直接导入。教程文件是我们在安装Tensorflow时自动添加的。这里我们直接将数据从中导入。python中的实现如下:1
2from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot = True)
这个代码在运行时会在当前目录下生成一个名为“MNIST_data”的文件夹,并在此文件夹中导入MNIST数据。一共得到四个文件,分别是训练数据、训练标签、测试数据以及测试标签。在接下来的代码中它们可以分别通过mnist.train.images、minst.train.labels、mnist.test.images、mnist.test.labels来调用,非常方便。
函数中的one-hot是针对数据标签的操作。它可以将表示分类的标签y转换为一个只有第y项为1,其余项都为0,且项数为总分类数的向量。这样操作之后,向量的每一项代表了一个分类,当数据属于一个分类时,该分类所属项为1,其余项为0。以此可以更加方便地计算代价函数。举个例子:MNIST数据集一共有10个分类(数字0~9),那么数字3的标签就会转换为[0,0,0,1,0,0,0,0,0,0]。
softmax回归
softmax回归比较简单。它相当于在线性模型后增加了一个softmax函数,将线性模型的输出转换到[0,1]区间中,并且使各个类别的输出值相加为1,因此它可以被当成是某个分类的概率。softmax回归模型最终输出为一个向量,其项数为总分类数,并且每项代表一个分类的概率。这与one-hot输出的形式是一样的。
定义张量
MNIST的数据x与标签y_为模型的输入,因此使用placeholder类别;而模型参数W与b需要通过数据集训练得到,因此使用Variable类别。定义它们并将其初始化为0。实现代码如下:1
2
3
4
5#定义张量
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
构建computational graph
softmax回归模型由一个线性模型及softmax函数组成,其输出表达式为:
其中W与b相乘为矩阵相乘。在Tensorflow中矩阵相乘不能使用普通的乘号,也不能用numpy的函数,必须使用Tensorflow内置的矩阵乘法函数:tf.matmul(mat1, mat2)。softmax函数可以直接使用Tensorflow函数tf.nn.softmax()实现。tf.nn模块包含了几乎所有神经网络要用到的函数,因此之后会经常用到它(官方文档)。输出y的实现代码如下:1
2#构建computational graph
y = tf.nn.softmax(tf.matmul(x, W) + b)
我们选择交叉熵函数(cross-entropy)作为代价函数,它是在信息学中最先被提出的。其定义为:
求出每个样本的交叉熵后,再对它们求平均值,便得到了损失值。将其表示为代码:1
2#代价函数
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices = [1]))
其中tf.reduce_sum(input_tensor, axis, reduction_indices)为Tensorflow的求和函数(官方文档),reduction_indices = [1]代表将输入的第二个维度相加,与axis作用一致。tf.reduce_mean(input_tensor, axis)为Tensorflow的均值函数(官方文档)。
而实际上Tensorflow在tf.nn中已经提供了直接求交叉熵代价函数的方程,由于该函数包含了softmax步骤,因此可以将之前的代码改为:1
2
3
4#构建computational graph
y = tf.matmul(x, W) + b
#代价函数
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = y, labels = y_))
其中logits为模型输出值,labels为实际标签值。
训练参数
设置训练目标,这里选用梯度下降法,学习率为0.5,训练目标为降低损失值cross_entropy:1
2#设置训练目标
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
设置Session,初始化Variable,之后使用分批训练的方式,每100个数据为一个batch,通过for循环运行1000次,得到预测模型:1
2
3
4
5
6
7
8
9#设置Session
sess = tf.Session()
#Variable初始化
init = tf.global_variables_initializer()
sess.run(init)
#分批训练
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100) #mnist.train.next_batch()函数得到下一batch的数据
sess.run(train_step, feed_dict = {x: batch_xs, y_: batch_ys}) #使用该批次训练
评估模型
训练完模型后就可以使用测试数据集来测试模型的精确度了。首先定义精确度,它等于识别正确的数量除以测试总数。精确度可以采用以下代码实现:1
2
3#评估模型
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) #判断是否识别正确
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) #计算精确度
其中tf.argmax(input, axis)函数(官方文档)为返回一个向量最大值的坐标,第二个参数1表示在向量第二维寻找最大值并返回其坐标(correct_prediction[n][10]第一维n为样本数量,第二维为每个样本的输出)。使用tf.argmax()分别得到模型测试的类别以及真实标签的类别。再使用tf.equal(x, y)函数(官方文档)比较它们,得到一系列布尔值的矩阵。它代表预测的分类与实际的分类相同与否,并以此来判断识别是否正确。
tf.cast(x, dtype)函数(官方文档)在这里的作用是将布尔值转换为浮点数。最后用均值函数求取均值就得到了模型的测试精确度。
通过Session运行并输出:1
2#输出
print("accuracy:", sess.run(accuracy, feed_dict = {x: mnist.test.images, y_:mnist.test.labels}))
最终得到模型的精确度为:0.92121
accuracy: 0.9212
0.92的精确度显然不能令我们满意,毕竟这只是一个十个数字符号的识别任务。softmax回归模型过于简单,没有考虑图像像素的位置关系。接下来我们将使用一个简单的卷积神经网络来大幅提升精确度。
卷积神经网络
卷积神经网络(Convolutional Neural Network: CNN)常被用于图像的识别,它考虑了输入数据的二维或三维(可能更高)结构,因此对于数字字符图像这样的识别对象非常有效。
网络结构
在这里我们要建立一个包含两个卷积层的卷积神经网络,并在训练时使用dropout。网络的前向传播过程为:输入数据经过reshape变形为二维图形数据,输入一个filter为5×5,步长为1,padding为same的卷积层,经过relu激活函数后输入一个步长为2,padding为same的max池化层。再经过一个相同的卷积层+relu+池化层组合后,将输出变形为一个列向量,输入一个全连接层。该全连接层输出为一个项数为1024的向量。之后经过dropout后再将其输入至另一个1024×10的全连接层,最终得到一个1×10的向量,即输出向量。整个卷积神经网络结构如下: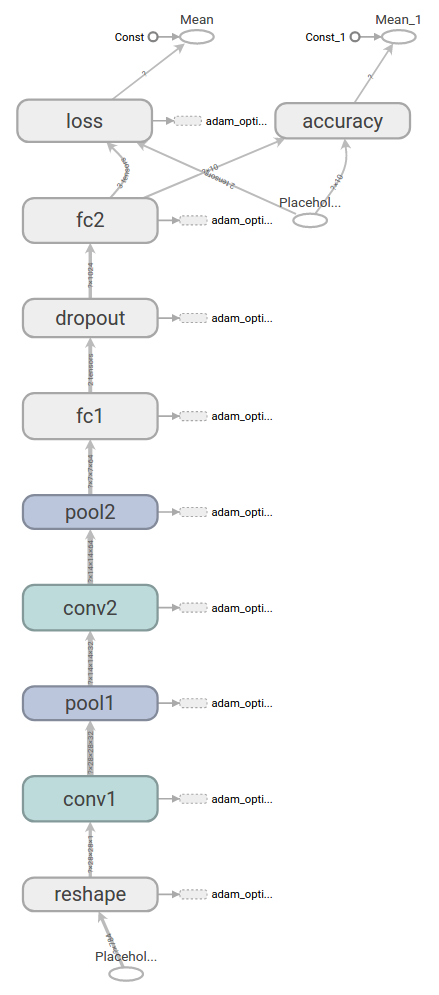
定义张量
卷积神经网络由于有多个层,每个层都会有权重W和偏差b。在这里我们不像之前那样将它们全部初始化为0,而是初始化为一些很小的随机数,因为在深度网络中全部初始化为0会造成梯度上的一些问题。为了方便起见,我们将W及b的定义与初始化放入函数中,这样可以使代码更加美观直接:1
2
3
4
5
6
7
8
9#定义W初始化函数
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev = 0.1)
return tf.Variable(initial)
#定义b初始化函数
def bias_variable(shape):
initial = tf.constant(0.1, shape = shape)
return tf.Variable(initial)
初始化权重时,我们使用了tf.truncated_normal(shape, mean, stddev)函数(官方文档),其中shape代表生成张量的维度,mean代表均值,stddev代表标准差。与tf.random_normal()不同,它是从截断的正太分布中输出维度为shape的随机数,且该正太分布服从均值为mean,标准差为stddev。截断的意思指生成的随机数不能离均值太远,只能在[μ-2σ,μ+2σ]之间取值。若生成的随机数超过了这个区间,则函数会自动舍弃并重新生成,这保证了参数的初始值不会太大。因此它经常被用来初始化训练参数。参数初始化后使用tf.Variable()定义张量。
初始化偏差时,我们将它们统一初始化为0.1,再定义Variable张量即可。
定义完函数后我们将使用它们对各个模型参数进行定义和初始化,同时定义x与y_。每个卷积层和全连接层都有一个W和一个b,而池化层没有参数,定义时要注意它们的维度计算。除此之外我们还需要定义dropout的概率参数,因为在训练模型和评估模型时它们的值是不同的。代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16#定义张量
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
#初始化W,b
W_conv1 = weight_variable([5, 5, 1, 32]) #第一个卷积层权重
b_conv1 = bias_variable([32]) #第一个卷积层偏差
W_conv2 = weight_variable([5, 5, 32, 64]) #第二个卷积层权重
b_conv2 = bias_variable([64]) #第二个卷积层偏差
W_fc1 = weight_variable([7 * 7 * 64, 1024]) #第一个全连接层权重
b_fc1 = bias_variable([1024]) #第一个全连接层偏差
W_fc2 = weight_variable([1024, 10]) #第二个全连接层权重
b_fc2 = bias_variable([10]) #第二个全连接层偏差
#定义dropout参数
keep_prob = tf.placeholder(tf.float32)
构建computational graph
根据之前规划的网络结构来构建computational graph。卷积神经网络的各个层都可以使用tf.nn模块中定义的函数实现。这里我们使用的函数如下:
tf.nn.conv2d(input, filter, strides, padding)(官方文档):使用filter对输入input进行卷积,其卷积的步长为strides,padding为padding。
tf.nn.relu(feature)(官方文档):对输入feature进行relu运算。
tf.nn.max_pool(value, ksize, strides, padding)(官方文档):使用ksize设定的窗对输入value进行池化运算,其步长为strides,padding为padding。
全连接层没有专门的函数,直接使用Tensorflow的矩阵运算就可以了。构建网络的代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13#构建computational graph
x_image = tf.reshape(x, [-1, 28, 28, 1])
Z1 = tf.nn.conv2d(x_image, W_conv1, strides = [1, 1, 1, 1], padding = 'SAME') + b_conv1
A1 = tf.nn.relu(Z1)
P1 = tf.nn.max_pool(A1, ksize = [1, 2, 2, 1], strides = [1, 2, 2, 1], padding = 'SAME')
Z2 = tf.nn.conv2d(P1, W_conv2, strides = [1, 1, 1, 1], padding = 'SAME') + b_conv2
A2 = tf.nn.relu(Z2)
P2 = tf.nn.max_pool(A2, ksize = [1, 2, 2, 1], strides = [1, 2, 2, 1], padding = 'SAME')
P2_flat = tf.reshape(P2, [-1, 7 * 7 * 64])
Z3 = tf.matmul(P2_flat, W_fc1) + b_fc1
A3 = tf.nn.relu(Z3)
D1 = tf.nn.dropout(A3, keep_prob)
y = tf.matmul(D1, W_fc2) + b_fc2
最后定义代价函数,其方法与softmax回归模型一致:1
2#定义代价函数
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels = y_, logits = y))
设置训练目标与评价参数
在这里我们使用Adam的优化方法来降低代价函数的损失值。在这里要注意的是,程序中对Variable的初始化要在Adam定义之后,不然会报错,这可能是因为Adam的函数中本身也定义了一些Variable需要初始化。因此在写Tensorflow时我都习惯将初始化的代码放在训练之前。代码如下:1
2#设置训练目标
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
若我们希望训练过程中输出模型的精确度,则需要在训练之前设置评估参数。其设置方法与softmax回归模型一致:1
2
3#设置评估参数
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
训练参数
在初始化Variable之后使用for循环对参数进行训练,其实现过程与softmax类似。由于网络参数较多,我们每次使用数据量为50的batch迭代20000次。并且每迭代1000次输出模型对训练集的精确度。其实现代码如下:1
2
3
4
5
6
7
8
9
10
11#Variable初始化
init = tf.global_variables_initializer()
sess.run(init)
#循环训练
for i in range(20000):
batch_xs, batch_ys = mnist.train.next_batch(50)
sess.run(train_step, feed_dict = {x: batch_xs, y_: batch_ys, keep_prob: 0.5})
if i % 1000 == 0:
train_accuracy = sess.run(accuracy, feed_dict = {x: batch_xs, y_: batch_ys, keep_prob: 1})
print("step", i, "training accuracy:",train_accuracy)
评估模型
最后使用测试集对模型进行评估并输出最终精确度:1
2
3
4#输出
test_accuracy = sess.run(accuracy, feed_dict = {x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1})
print("test accuracy:", test_accuracy)
sess.close()
这样就已经大功告成啦!打开终端运行代码,整个训练过程可能要持续半小时或者更久(由你CPU或GPU水平决定)。休息下喝杯茶吧!
最终的输出为:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21step 0 training accuracy: 0.04
step 1000 training accuracy: 0.96
step 2000 training accuracy: 1.0
step 3000 training accuracy: 1.0
step 4000 training accuracy: 0.98
step 5000 training accuracy: 1.0
step 6000 training accuracy: 1.0
step 7000 training accuracy: 1.0
step 8000 training accuracy: 1.0
step 9000 training accuracy: 1.0
step 10000 training accuracy: 1.0
step 11000 training accuracy: 1.0
step 12000 training accuracy: 1.0
step 13000 training accuracy: 1.0
step 14000 training accuracy: 1.0
step 15000 training accuracy: 1.0
step 16000 training accuracy: 1.0
step 17000 training accuracy: 1.0
step 18000 training accuracy: 1.0
step 19000 training accuracy: 1.0
test accuracy: 0.9918
每个人得到的结果会略有不同,因为参数初始化时是随机的,但大致都在99.2%左右,比softmax回归模型提高了很多!
小结
- 认识MNIST数据集
- 定义一个softmax回归模型,训练后得到最终精确度为92%
- 使用tf.nn中的函数能方便地定义一个卷积神经网络,训练后得到最终精确度为99.2%,相比softmax回归模型有了大幅的提升。