支持向量机（四）

  到目前为止，我们把SVM优化问题化为了更容易解决的对偶问题，并且使用核函数及正则化来改善它的特性。现在我们只需解决这个对偶问题就可以得到最优间隔分类器，可以说是“万事具备，只欠东风”了。我们先将第三章节得到的对偶问题搬运过来：

$$\begin{eqnarray} \max_{\alpha}\ &&\theta_{\cal{D}}(\alpha)=\sum_{i=1}^m\alpha_i-{1 \over 2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_j\langle x^{(i)},x^{(j)}\rangle\tag{1}\\ {\rm s.t.}\ &&0\leq\alpha_i\leq C,\ i=1,...,m\tag{2}\\ &&\sum_{i=1}^m\alpha_iy^{(i)}=0\tag{3} \end{eqnarray}$$

  在机器学习中，求函数极值点常用的方法除了常规的求导，就是梯度下降法了。但式(1)(2)(3)所示的对偶问题对所有参数均有约束。若使用梯度下降法，在每次更新权重时还需要保持所有参数都满足约束，这是难以做到的。1998年，John C.Platt的论文Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines针对上述问题提出了SMO（sequential minimal optimization）算法，它能够很好地解决并快速求解出SVM的最优解。

坐标下降法

  为了引入SMO算法，我们来看一个相似的算法——坐标下降法（coordinate ascent）。考虑如下无约束优化问题：

$$\max_{\alpha}W(\alpha_1,\alpha_2,...,\alpha_m)$$

  其中$W$是以$\alpha_1,…,\alpha_m$为参数的函数。坐标下降法求取极值的过程如下：
    循环直到收敛：$\{$
      ${\rm For}\ i=1,…,m\{$
        $\alpha_i:=\arg{\rm max}_{\hat{\alpha_i}}W(\alpha_1,…,\alpha_{i-1},\hat{\alpha_i},\alpha_{i+1},…,\alpha_m)$
      $\}$
    $\}$

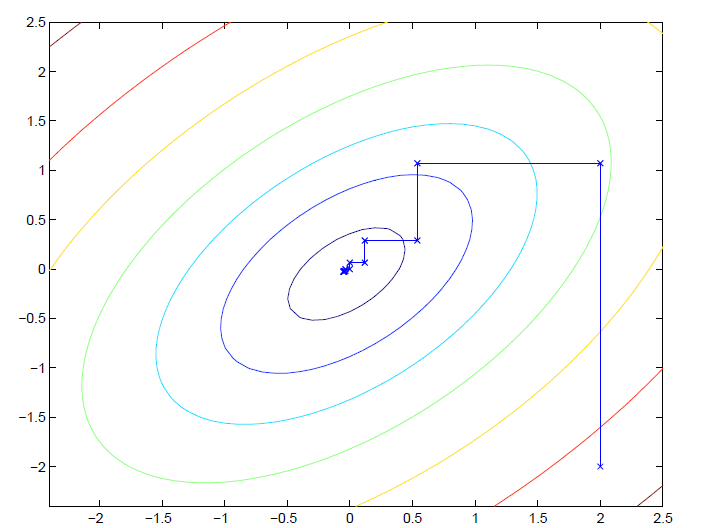
  其中$\arg\max$表示使式子达到最大值时变量的取值。在上述算法中，每次迭代我们只更新其中一个参数而保持其他参数不变，并且参数更新的顺序是它们下标的顺序，这就是坐标下降法。当然我们也可以按照一定规则来选择更新的参数，比方说每次更新选择梯度最大的参数。下图为一个简单的例子：

  图中的椭圆为优化函数的等高线。参数初始值为$(2,-2)$。我们每次只更新其中一个参数，在经过数次更新后，函数值趋向于全局最大值。

SMO算法

  现在让我们来看式(1)(2)(3)所表示的对偶问题。若我们使用坐标下降法，保持$\alpha_2,…,\alpha_m$不变并且更新$\alpha_1$，就会出现问题：由于式(3)的约束，因此有：

$$\alpha_1y^{(1)}=-\sum_{i=2}^m\alpha_iy^{(i)}\tag{4}$$

  等式两边同时乘以$y^{(1)}$得到：

$$\alpha_1=-y^{(1)}\sum_{i=2}^m\alpha_iy^{(i)}\tag{5}$$

  我们发现$\alpha_1$已经被约束条件限制住了。如果$\alpha_2,…,\alpha_m$不变，那么$\alpha_1$就不能改变。因此只更新一个参数是行不通的，我们必须同时更新两个以上的参数。在此引出SMO算法：

    循环直到收敛：$\{$
      1. 选取参数对$\alpha_i$与$\alpha_j$（使用启发式方法选取参数对）
      2. 更新$\alpha_i$与$\alpha_j$，并保持其他参数不变
    $\}$

更新参数对

  更新参数时要注意，更新后的参数必须满足KKT条件。下面以更新$\alpha_1,\alpha_2$为例来说明SMO算法的思想。根据式(3)，我们得到一个$\alpha_1$与$\alpha_2$所满足的方程：

$$\alpha_1y^{(1)}+\alpha_2y^{(2)}=-\sum_{i=3}^m\alpha_iy^{(i)}=\zeta\tag{6}$$

  由于$\alpha_3,…,\alpha_m$固定，因此$\zeta$为一个常值。根据式(6)，$\alpha_1$可以表示为$\alpha_2$的函数：

$$\alpha_1=(\zeta-\alpha_2y^{(2)})y^{(1)}\tag{7}$$

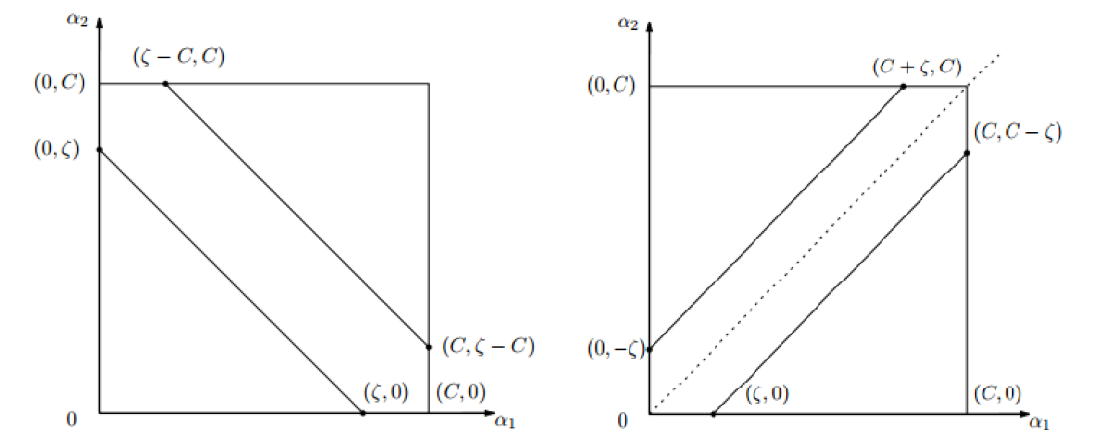
  函数在$\alpha_1,\alpha_2$坐标系下表示为一条直线，并且它根据$y^{(1)},y^{(2)}$是否相等分为以下两种情况：

  根据式(2)，我们知道$\alpha_1,\alpha_2$的取值只能在上图中$[0,C]\times [0,C]$的方框中，而它们又满足方程$\alpha_1y^{(1)}+\alpha_2^{(2)}y^{(2)}=\zeta$，因此根据图像可以得到$\alpha_2$的取值范围，记为$[L,H]$。
  准备工作做完后，我们开始优化式(1)。将式(7)带入式(1)中得到：

$$\theta_{\cal{D}}(\alpha_1,\alpha_2,...,\alpha_m)=\theta_{\cal{D}}((\zeta-\alpha_2y^{(2)})y^{(1)},\alpha_2,...,\alpha_m)\tag{8}$$

  式(8)将优化目标变为了$\alpha_2$的函数。若观察式(1)我们发现式中只有$\alpha_i$与$\alpha_i\alpha_j$项，因此式(8)可以表示为$a\alpha_2^2+b\alpha_2+c$的形式，是一个抛物线。这时问题就转化为了在$[L,H]$区间中求抛物线的极值。我们令$\alpha_2^{temp}$为抛物线的最值点（此时$\alpha_2^{temp}$不一定在$[L,H]$内），则$[L,H]$区间中抛物线的极值点$\alpha_2^{new}$为：

$$\alpha_2^{new}=\begin{cases} H\ &,\alpha_2^{temp}>H\\ \alpha_2^{temp}\ &,L\leq\alpha_2^{temp}\leq H\\ L\ &,\alpha_2^{temp}<L \end{cases}$$

  根据式(7)求出$\alpha_1^{new}$：

$$\alpha_1^{new}=(\zeta-\alpha_2^{new}y^{(2)})y^{(1)}$$

更新偏差值$b$

  更新$\alpha$值后。我们需要调整$b$的值使得解满足KKT条件。这里将第三章节最后的三种情况重新罗列在下面：

$$\begin{eqnarray} \alpha_i=0&\Leftrightarrow& y^{(i)}(w^Tx^{(i)}+b)\geq 1\tag{9}\\ \alpha_i=C&\Leftrightarrow& y^{(i)}(w^Tx^{(i)}+b)\leq 1\tag{10}\\ 0<\alpha_i<C&\Leftrightarrow& y^{(i)}(w^Tx^{(i)}+b)= 1\tag{11}\\ \end{eqnarray}$$

  若$0<\alpha_1^{new}<C$，通过式(11)可求得满足KKT条件的$b_1$（此时$\alpha_1,\alpha_2$值已更新）：

$$b_1=y^{(1)}-\sum_{i=1}^m\alpha_iy^{(i)}\langle x^{(i)},x^{(1)}\rangle\tag{12}$$

  若$0<\alpha_2^{new}<C$，同样可求得$b_2$：

$$b_2=y^{(2)}-\sum_{i=1}^m\alpha_iy^{(i)}\langle x^{(i)},x^{(2)}\rangle\tag{13}$$

  若$0<\alpha_1^{new}<C$与$0<\alpha_2^{new}<C$同时满足，则$\alpha_2^{new}$未经过区间$[L,H]$的裁剪，为式(8)的最值点，满足：

$${\partial\theta_{\cal{D}} \over \partial\alpha_2}={\partial\alpha_1 \over \partial\alpha_2}+1-\sum_{i=1}^my^{(1)}y^{(i)}{\partial\alpha_1 \over \partial\alpha_2}\alpha_i\langle x^{(1)},x^{(i)}\rangle-\sum_{i=1}^my^{(2)}y^{(i)}\alpha_i\langle x^{(2)},x^{(i)}\rangle=0$$

  其中偏微分项由式(7)得到：

$${\partial\alpha_1 \over \partial\alpha_2}=-y^{(1)}y^{(2)}$$

  带回原式：

$$-y^{(1)}y^{(2)}+1+\sum_{i=1}^my^{(2)}y^{(i)}\alpha_i\langle x^{(1)},x^{(i)}\rangle-\sum_{i=1}^my^{(2)}y^{(i)}\alpha_i\langle x^{(2)},x^{(i)}\rangle=0$$

  等式两边同时乘以$y^{(2)}$，整理后得到：

$$y^{(1)}-\sum_{i=1}^m\alpha_iy^{(i)}\langle x^{(i)},x^{(1)}\rangle=y^{(2)}-\sum_{i=1}^m\alpha_iy^{(i)}\langle x^{(i)},x^{(2)}\rangle$$

  带入式(12)(13)，我们发现，若$0<\alpha_1^{new}<C$与$0<\alpha_2^{new}<C$同时满足，则必有：

$$b_1=b_2\tag{14}$$

  若$0<\alpha_1^{new}<C$与$0<\alpha_2^{new}<C$同时不满足，则$\alpha_1^{new},\alpha_2^{new}$为$0$或$C$。根据式(9)(10)，得到$b$的取值范围$[b_1,b_2]$。$b^{new}$可以取其中任意值，通常取：

$$b^{new}={b_1+b_2 \over 2}\tag{15}$$

  综合式(12)~(15)四种情况，我们得到$b^{new}$的取值为：

$$b^{new}=\begin{cases} b_1,&0<\alpha_1^{new}<C\\ b_2,&0<\alpha_2^{new}<C\\ (b_1+b_2)/2&其他 \end{cases}$$

  更新完$b$后，就算完成了一次迭代。重复这个过程，一直循环到收敛，就得到对偶问题的最优解了。

选择参数对

  在算法刚开始时，$\alpha$值初始化为$[0,C]$区间中的随机数，因此必然有很多$\alpha$值不满足KKT条件。而我们算法的目标是使得所有$\alpha$满足KKT条件，因此在选择第一个参数$\alpha_i$时，算法会遍历整个训练集，找到不满足KKT条件的训练样本，并将它设为需要更新的参数。
  得到第一个参数$\alpha_i$后，算法会选择第二个参数$\alpha_j$来最大化优化步长。因此算法会遍历所有非边界样本（即满足$0<\alpha_i<C$的样本），找到第二个参数$\alpha_j$使得$|E_i-E_j|$最大。其中$E$为训练样本预测值与实际值的偏差：

$$E_i=w^Tx^{(i)}+b-y^{(i)}$$

  若$E_i$是正偏差，则在所有负偏差中找到最小的$E_j$；若$E_i$是负偏差，则在所有正偏差中找到最大的$E_j$。这样就选择出了需要更新的参数对$\alpha_i,\alpha_j$。

小结

1. 坐标下降法每次只更新一个参数而固定其他所有参数。
2. SMO算法每次更新一个参数对，同时更新$b$使它们满足KKT条件。
3. 使用启发式方法选择每次更新的参数对。

  到这里SVM就算告一段落了，这是我大二时候学习的内容，如今再看一遍还是有很多收获的，之前一些模糊的概念也都算理清楚了，完结撒花！