K-Means聚类算法(k-means clustering algorithm)是一种无监督学习算法。它可以通过多次迭代,将一系列无标记的数据根据它们的特征分布划分为$k$个子集,使得子集内部元素之间的相异度尽可能低,而不同子集元素相异度尽可能高。我们称这样的子集为簇(cluster),而将数据划分为簇的过程称为聚类。
算法思想
假设我们有一组无标记的训练样本$\{x^{(1)},…,x^{(m)}\},\ x\in{\Bbb R^n}$,使用K-Means聚类算法将它们划分过程如下:
1. 随机初始化簇中心(cluster centroid)$\mu_1,…,\mu_k\in{\Bbb R}$
2. 循环直到收敛:$\{$
${\rm For}\ i=1,…,m\{$
$\}$
${\rm For}\ j=1,…,k\{$
$\}$
$\}$
其中$k$是我们想要划分的簇数,$c^{(i)}$表示当前迭代中第$i$个样本所在的簇($c^{(i)}=1$就代表$x^{(i)}$属于第$1$个簇),$\mu_j$表示当前迭代中第$j$个簇的中心。
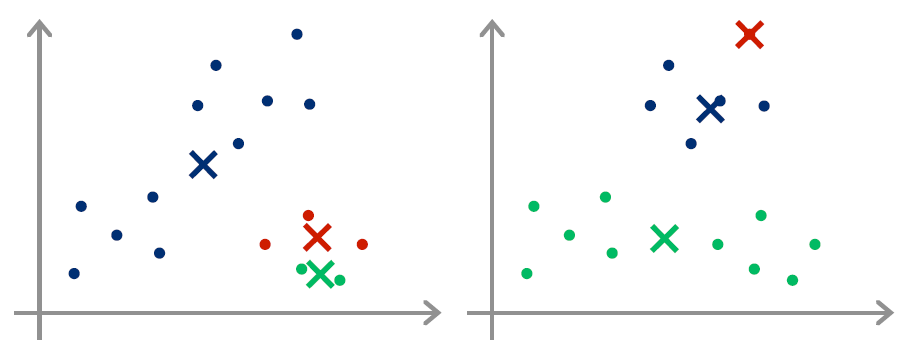
整个算法思想大致是:首先为每一个簇初始化簇中心,我们有$k$个簇因此有$k$个簇中心。再使用训练集对簇中心进行迭代。迭代过程中,先将每一个样本分配给与其距离最小的簇中心所对应的簇,这样就相当于对样本进行了一次划分,构建了$k$个簇。再将每个簇中样本的算数平均值作为新的簇中心。不断进行这样的迭代直到簇中心不再变化,此时对样本的划分也不再改变。此时我们就得到了样本的$k$个簇。下面的举例能够很好地说明整个算法的过程:
图中(a)表示原始数据集;(b)表示随机初始化簇中心;(c)表示将样本分配给簇;(d)表示根据(c)中样本分配得到新的簇中心;(e)(f)表示用相同方法迭代直至收敛。
在实际中,我们通常不会像上图举例那样对簇中心进行初始化,而是随机选择$k$个样本作为初始的簇中心(此时需保证$k<m$),这样能使算法更快地收敛。
失真函数
为了更好地描述簇划分的好坏,我们引入失真函数(distortion function)$J$,它表示簇中样本与簇中心的相异度:
其中$\mu_{c^{(i)} }$表示第$i$个样本所在簇的簇中心,因此$J$计算的是样本与其所在簇的簇中心距离的平方和。$J$越小表示相异度越小,对样本的划分越好。现在再回头看,我们会发现,算法中迭代的每一步都是在保持一部分参数不变的情况下,使用另一部分参数来最小化失真函数。因此在K-Means聚类算法运行过程中,失真函数只会减小不会增加,这也可以被用来检验算法程序是否由BUG。
由于失真函数是一个非凸函数,因此不能保证每次算法都给出一个全局最小值,可能存在下图所示的局部最小值情况:
因此在实际中我们常常使用不同的随机初始值运行若干次算法,并找出失真函数值最小的那个作为样本的划分。
$k$的选择
我们之前的讨论都是在给定$k$的情况下进行的。但面对一组数据集时,通常很难判断$k$到底取多少合适。下面的方法可以一定程度上帮助我们判断$k$的取值。
Elbow方法
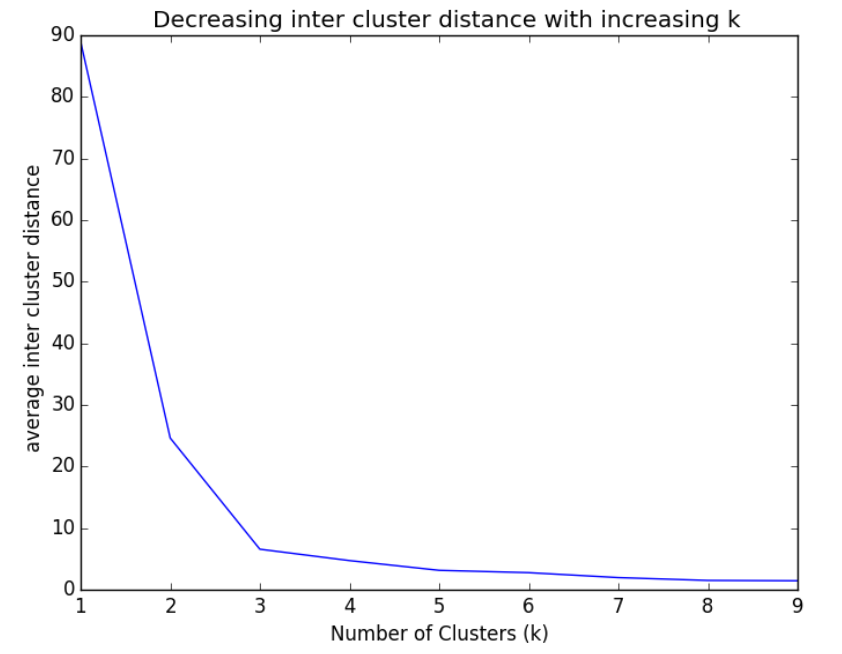
Elbow方法(Elbow method)是由Robert Tibshirani、Guenther Walther与Trevor Hastie于2000年提出的。它的思想很简单:从1开始尝试使用不同的$k$值对数据集进行K-Means聚类,运行后每个$k$值对应一个失真函数。以$k$值为横坐标,失真函数值$J$为纵坐标作折线图,得到一个单调递减的曲线。若曲线中存在一个明显的拐点(如下图所示,此时$k=3$),则取其中拐点对应的$k$值作为我们的选择。
由于此时图中曲线像人的手臂,而拐点就相当于肘部,因此该方法被称为Elbow方法。但很多时候曲线并没有明显的拐点,该方法就无法奏效。实际中我们只会将它作为一种尝试,并不会对它报太大的期望。
通过实际目的选择
通常我们对数据分类是有一定目的的,因此可以根据实际目的对$k$进行选择。换句话说,就是我觉得分几类好就分几类。
比如T恤尺寸问题:我们需要设计$k$种T恤尺寸来供应市场。现在有一批不同人身高体重的数据,我们将它们分为$k$类,并将每一类的簇中心取值作为该类T恤的标准尺寸。此时$k$的取值可以为3(S、M、L),也可以为5(XS、S、M、L、XL),这完全取决于市场以及生产成本,是通过实际目的进行选择的。
大多数情况下我们都会采用这种方法来选择$k$。因为根据丑小鸭定理(The Ugly Duckling Theorem),所有无标记的数据都是同等独特的,只有根据实际目的对它们的分类才有意义。
小结
- K-Means聚类算法可以自动将数据分为$k$类。
- 失真函数是簇划分好坏的判断标准。
- $k$值可以通过Elbow方法以及根据实际目的选择,大多数情况我们选择后者。