分布参数系统控制（七）：边界输入

  分布参数系统的输入可以分为点输入、分布式输入和边界输入。之前的章节我们讨论的都是分布式输入，此时输入分布在定义域的某个区间。而若输入$u(t)$定义在边界，则称为边界输入（Randeingriff），此时系统方程会有所不同，相应的计算方法也会有差别。因此本文讨论边界输入以及它在反馈控制中的应用。

边界输入

系统方程

  分布式输入中，输入$u(t)$在系统状态方程中；而边界输入中，$u(t)$在系统边界条件中。一个典型的边界输入系统如下：

$$\begin{eqnarray} \partial_tx(z,t)&=&{\cal A}x(z,t),\ t>0,\ z\in(0,1)\tag{1}\\ x(0,t)&=&0,\ t>0\tag{2}\\ x(1,t)&=&u(t),\ t>0\tag{3}\\ x(z,0)&=&x_0(z),\ z\in[0,1]\tag{4} \end{eqnarray}$$

  其中式(3)边界条件表示输入为$z=1$处的边界输入，同时式(4)所示的初始条件需要满足式(2)(3)的边界条件，即：

$$\begin{eqnarray} x_0(0)&=&0\\ x_0(1)&=&u(0) \end{eqnarray}$$

分布式输入转换

  在不改变系统的前提下，我们可以使用特殊的方法将边界输入系统转换为分布式输入。以式(1)~(4)所示系统为例，设${\cal A}h={\rm d}_z^2h$。首先将系统状态变量分解：

$$x(z,t)=x_H(z,t)+x_I(z,t)\tag{5}$$

  其中$x_H(z,t)$满足齐次边界条件：

$$\begin{eqnarray} x_H(0,t)&=&0\tag{6}\\ x_H(1,t)&=&0\tag{7} \end{eqnarray}$$

  $x_I(z,t)$满足非齐次边界条件：

$$\begin{eqnarray} x_I(0,t)&=&0\tag{8}\\ x_I(1,t)&=&u(t)\tag{9} \end{eqnarray}$$

  简单来说齐次边界条件就是输入$u(t)$不存在时的边界条件；非齐次边界条件就是$u(t)$存在时的边界条件。这有点像零输入响应与零状态响应，不过还是有区别的。
  非齐次部分$x_I(z,t)$可以表示为一个多项式$f(z)$与$u(t)$的乘积:

$$x_I(z,t)=f(z)u(t)\tag{10}$$

  其中$f(z)$的阶数可以取到足够高为止。我们先假设$f(z)$为一阶：

$$f(z)=az+b\tag{11}$$

  通过式(8)(9)可以求解出$f(z)$：

$$\begin{eqnarray} x_I(0,t)&=&f(0)u(t)=bu(t)=0\\ x_I(1,t)&=&f(1)u(t)=(a+b)u(t)=u(t) \end{eqnarray}$$

  我们得到$a=1,b=0$（若无法求解，则增加$f(z)$的阶数）。此时：

$$x_I(z,t)=zu(t)\tag{12}$$

  将式(12)带入式(1)，就可以得到一个$x_H(z,t)$的方程：

$$\begin{eqnarray} &&\partial_t(x_H(z,t)+x_I(z,t))=\partial_z^2(x_H(z,t)+x_I(z,t))\\ \Rightarrow&&\partial_t(x_H(z,t)+zu(t))=\partial_z^2(x_H(z,t)+zu(t))\\ \Rightarrow&&\partial_tx_H(z,t)=\partial_z^2x_H(z,t)-z\partial_tu(t) \end{eqnarray}$$

  将式(6)(7)的边界条件以及相应初始条件加入后，我们便将原系统转换为了$x_H(z,t)$为状态变量的分布式输入系统：

$$\begin{eqnarray} \partial_tx_H(z,t)&=&{\cal A}x_H(z,t)-z\partial_tu(t),\ t>0,\ z\in(0,1)\\ x_H(0,t)&=&0,\ t>0\\ x_H(1,t)&=&0,\ t>0\\ x_H(z,0)&=&x_0(z)-zu(0),\ z\in[0,1] \end{eqnarray}$$

反馈控制（Backstepping）

  若不转换为分布式输入，我们也可使用Backstepping来设计边界输入的反馈控制。这种控制方法来源于非线性控制（详见Backstepping（反步控制）），但个人觉得两者差别还是挺大的。

基本思路

  Backstepping基本思路如下：
  1. 识别系统中不稳定的状态。
  2. 选择所要达到的稳定目标系统。
  3. 计算Backstepping变换以达到目标。
  4. 通过Backstepping得到Backstepping控制器。
  下面我们将通过一个例子来分步演示Backstepping的设计过程。

识别系统不稳定状态

  我们仍然以式(1)~(4)所示系统为例，并设系统算子为${\cal A}h=\partial_z^2h+\gamma h,$ $\gamma>\pi^2$。系统表示如下：

$$\begin{eqnarray} \partial_tx(z,t)&=&\partial_z^2x(z,t)+\gamma x(z,t),\ t>0,\ z\in(0,1),\tag{13}\\ x(0,t)&=&0,\ t>0\tag{14}\\ x(1,t)&=&u(t),\ t>0\tag{15}\\ x(z,0)&=&x_0(z),\ z\in[0,1]\tag{16} \end{eqnarray}$$

  计算系统特征值，我们得到$\lambda_i=\gamma-(i\pi)^2$。系统存在部分特征值实部大于零，不稳定。又系统只有一个状态变量$x(z,t)$，因此我们的目标就是将$x(z,t)$通过反馈转换为稳定状态。

选择目标系统

  根据第三章节式(13)：

$$x(t)=\sum_{i=1}^{\infty}e^{\lambda_it}\phi_ix_i^\ast (0)$$

  可以发现，若我们将$x(t)$乘以一个指数函数$e^{-\mu t}$，只要$\mu$足够大，则结果一定收敛。因此我们设目标状态变量为：

$$\tilde{x}(z,t)=e^{-\mu t}x(z,t)$$

  对于目标变量来说：

$$\begin{eqnarray} &&\partial_t\tilde{x}(z,t)&=&-\mu e^{-\mu t}x(z,t)+e^{-\mu t}\partial_tx(z,t)\\ && &=&e^{-\mu t}(\partial_z^2x(z,t)-(\mu-\gamma)x(z,t))\\ && &=&\partial_z^2\tilde{x}(z,t)-(\mu-\gamma)\tilde{x}(z,t)\\ &&\tilde{x}(0,t)&=&e^{-\mu t}x(0,t)=0\\ &&\tilde{x}(1,t)&=&e^{-\mu t}x(1,t)=0 \end{eqnarray}$$

  最后一项成立，是系统齐次的要求，即目标系统是原系统通过输入$u(t)$得到的，故目标系统中不能再存在$u(t)$。设$\mu_R=\mu-\gamma$，就得到了目标系统：

$$\begin{eqnarray} &&\partial_t\tilde{x}(z,t)&=&\partial_z^2\tilde{x}(z,t)-\mu_R\tilde{x}(z,t),\ t>0,\ z\in(0,1)\tag{17}\\ &&\tilde{x}(0,t)&=&0,\ t>0\tag{18}\\ &&\tilde{x}(1,t)&=&0,\ t>0\tag{19} \end{eqnarray}$$

  当$\mu_R>-\pi^2$时，目标系统指数稳定。

Backstepping变换

  Backstepping变换表达式如下：

$$\tilde{x}(z,t)=x(z,t)-\int_0^z\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta\tag{20}$$

  其中积分核$\kappa(z,\zeta)$是变换的关键。
  将$z=1$带入得到：

$$\tilde{x}(1,t)=x(1,t)-\int_0^1\kappa(1,\zeta)x(\zeta,t){\rm d}\zeta\tag{21}$$

  结合式(15)(19)(21)，我们得到输入$u(t)$的表达式：

$$u(t)=\int_0^1\kappa(1,\zeta)x(\zeta,t){\rm d}\zeta\tag{22}$$

  因此我们现在要做的就是将式(20)的Backstepping变换带入目标系统方程，求出积分核$\kappa(z,\zeta)$，再带入式(22)就得到了输入函数$u(t)$。通过求得的$u(t)$，在理论上就可以将原系统控制为稳定的目标系统。下面我们开始计算积分核，该过程较为繁琐，故建议在安静的时候耐心推导一遍（用Latex打出来太不容易了！）。

建立核方程

  将式(20)带入式(17)，方程左侧为：

$$\begin{split} \partial_t\tilde{x}(z,t)=&\partial_tx(z,t)-\int_0^z\kappa(z,\zeta)\partial_tx(\zeta,t){\rm d}\zeta\\ =&\partial_z^2x(z,t)+\gamma x(z,t)-\int_0^z\kappa(z,\zeta)\partial_{\zeta}^2x(\zeta,t){\rm d}\zeta-\int_0^z\gamma\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta \end{split}$$

  方程右侧为：

$$\begin{split} \partial_z^2\tilde{x}(z,t)&-\mu_R\tilde{x}(z,t)=\\ &\partial_z^2x(z,t)-\partial_z^2\int_0^z\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta-\mu_Rx(z,t)+\int_0^z\mu_R\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta \end{split}$$

  之后将方程左侧与右侧联立得到：

$$\begin{split} &\partial_z^2x(z,t)+\gamma x(z,t)-\int_0^z\kappa(z,\zeta)\partial_{\zeta}^2x(\zeta,t){\rm d}\zeta-\int_0^z\gamma\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta\\ =&\partial_z^2x(z,t)-\partial_z^2\int_0^z\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta-\mu_Rx(z,t)+\int_0^z\mu_R\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta \end{split}$$

  将所有项移动到一边：

$$\begin{split} 0=&-\partial_z^2x(z,t)+\partial_z^2\int_0^z\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta+\mu_Rx(z,t)-\int_0^z\mu_R\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta\\ &+\partial_z^2x(z,t)+\gamma x(z,t)-\int_0^z\kappa(z,\zeta)\partial_{\zeta}^2x(\zeta,t){\rm d}\zeta-\int_0^z\gamma\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta \end{split}$$

  到了这一步我们需要处理其中两个个麻烦的项。它们分别为：

$$\begin{eqnarray} &&-\int_0^z\kappa(z,\zeta)\partial_{\zeta}^2x(\zeta,t){\rm d}\zeta\tag{23}\\ &&\partial_z^2\int_0^z\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta\tag{24} \end{eqnarray}$$

  我们可以通过分部积分法将式(23)展开得到：

$$\begin{split} &-&\int_0^z\kappa(z,\zeta)\partial_{\zeta}^2x(\zeta,t){\rm d}\zeta=-[\kappa(z,\zeta)\partial_{\zeta}x(\zeta,t)]_ 0^z+\int_0^z\partial_{\zeta}\kappa(z,\zeta)\partial_{\zeta}x(\zeta,t){\rm d}\zeta\\ &=&-[\kappa(z,\zeta)\partial_{\zeta}x(\zeta,t)]_ 0^z+[\partial_{\zeta}\kappa(z,\zeta)x(\zeta,t)]_ 0^z-\int_0^z\partial_{\zeta}^2\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta\\ &=&-\kappa(z,z)\partial_zx(z,t)+\kappa(z,0)\partial_zx(0,t)+\partial_{\zeta}\kappa(z,z)x(z,t)\\ &&-\partial_{\zeta}\kappa(z,0)x(0,t)-\int_0^z{\rm d}_{\zeta}^2\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta \end{split}$$

  对于式(24)我们直接使用求导计算即可：

$$\partial_z\int_0^z\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta=\kappa(z,z)x(z,t)+\int_0^z\partial_z\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta$$

  我们再求一次导，得到式(24)的表达式：

$$\begin{split} &\partial_z^2\int_0^z\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta=\partial_z\left(\kappa(z,z)x(z,t)+\int_0^z\partial_z\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta\right)\\ &={\rm d}_z\kappa(z,z)x(z,t)+\kappa(z,z)\partial_zx(z,t)+\partial_z\kappa(z,z)x(z,t)+\int_0^z\partial_z^2\kappa(z,\zeta)x(\zeta,t){\rm d}\zeta \end{split}$$

  在这里需要注意$\kappa(z,z)$的本质是$\kappa(z,\zeta)$，只是第二个参数$\zeta$为$z$的函数$\zeta(z)=z$。因此$\kappa(z,z)$的导数为：

$$\begin{split} {\rm d}_z\kappa(z,z)={\rm d}_z\kappa(z,\zeta(z))&=\partial_z\kappa(z,z){ {\rm d}z \over {\rm d}z}+\partial_{\zeta}\kappa(z,z){ {\rm d}\zeta \over {\rm d}z}\\ &=\partial_z\kappa(z,z)+\partial_{\zeta}\kappa(z,z) \end{split}$$

  将麻烦项的展开带入原方程，合并同类项得到：

$$\begin{split} 0&=({\rm d}_z\kappa(z,z)+\partial_z\kappa(z,z)+\partial_{\zeta}\kappa(z,z)+\mu_R+\gamma)x(z,t)\\ &+(\kappa(z,z)-\kappa(z,z))\partial_zx(z,t)\\ &+\int_0^z(\partial_z^2\kappa(z,\zeta)-\partial_{\zeta}\kappa(z,\zeta)-(\mu_R+\gamma)\kappa(z,\zeta))x(\zeta,t){\rm d}\zeta\\ &+\kappa(z,0)\partial_zx(0,t)+\partial_{\zeta}\kappa(z,0)x(0,t) \end{split}$$

  由于$x(z,t)$是状态变量，因此若需要上式始终为$0$，则需要将$x(z,t)$及其导数前的系数方程都设置为$0$，因此得到：

$$\begin{eqnarray} 2{\rm d}_z\kappa(z,z)+\mu&=&0\tag{25}\\ \partial_z^2\kappa(z,\zeta)-\partial_{\zeta}^2\kappa(z,\zeta)-\mu\kappa(z,\zeta)&=&0\tag{26}\\ \kappa(z,0)&=&0\tag{27} \end{eqnarray}$$

  考虑完式(17)的系统状态方程，我们再来看式(18)(19)的边界条件。将式(20)带入式(18)：

$$\tilde{x}(0,t)=x(0,t)-\int_0^0\kappa(0,\zeta)x(\zeta,t){\rm d}\zeta=0$$

  式(18)恒成立，而式(19)在之前计算$u(t)$时已经考虑过了。因此综上所述我们得到了所有积分核需要满足的条件，即式(25)~(27)，使用它们建立核方程（Kerngleichung）：

$$\begin{eqnarray} \partial_z^2\kappa(z,\zeta)-\partial_{\zeta}^2\kappa(z,\zeta)&=&\mu\kappa(z,\zeta),\ 0<\zeta<z<1\tag{28}\\ \kappa(z,0)&=&0\tag{29}\\ \kappa(z,z)&=&-{\mu \over 2}z\tag{30} \end{eqnarray}$$

  接下来我们只要求解核方程就能得到积分核的表达式了。

求解核方程

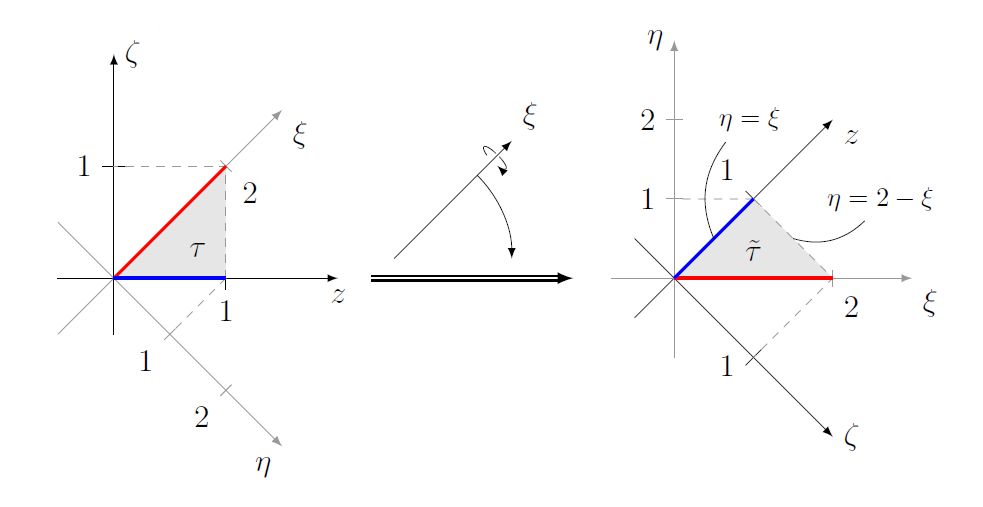
  可以发现式(28)所示的核方程是一个波动方程，我们通过坐标转换将它写成标准形式。引入坐标$\xi$与$\eta$：

$$\begin{cases} \xi=z+\zeta\\ \eta=z-\zeta \end{cases}$$

  由于原坐标存在约束条件$0<\zeta<z<1$，因此它的作用范围（Ortsbereich）在如下三条直线所围成的区域内：
  1. $\zeta=0$
  2. $\zeta=z$
  3. $z=1$
  通过坐标变换我们可以将这三条曲线转换为$\xi,\eta$坐标形式：
  1. $\begin{bmatrix}\xi\\\eta\end{bmatrix}_{\zeta=0}=\begin{bmatrix}1 && 1 \\ 1 && -1 \end{bmatrix}\begin{bmatrix}z\\0\end{bmatrix}=\begin{bmatrix} 1 \\ 1 \end{bmatrix}z\Rightarrow \xi=\eta$
  2. $\begin{bmatrix}\xi\\\eta\end{bmatrix}_{\zeta=z}=\begin{bmatrix}1 && 1 \\ 1 && -1 \end{bmatrix}\begin{bmatrix}z\\z\end{bmatrix}=\begin{bmatrix} 2 \\ 0 \end{bmatrix}z\Rightarrow \eta=0$
  3. $\begin{bmatrix}\xi\\\eta\end{bmatrix}_{z=1}=\begin{bmatrix}1 && 1 \\ 1 && -1 \end{bmatrix}\begin{bmatrix}1\\\zeta\end{bmatrix}=\begin{bmatrix} 1+\zeta \\ 1-\zeta \end{bmatrix}z\Rightarrow \xi+\eta=2$

  因此核方程作用范围${\cal T}_R$变化为$\tilde{\cal T}_R$，如下图所示：

  设核方程$\kappa(z,\zeta)$通过坐标变换转换为$G(\xi,\eta)$，即：

$$\kappa(z,\zeta)=G(\xi,\eta)=G(\xi(z,\zeta),\eta(z,\zeta))\tag{31}$$

  带入式(28)~(30)得到$G(\xi,\eta)$所满足的方程。其中：

$$\begin{eqnarray} \partial_z\kappa(z,\zeta)&=&\partial_{\xi}G(\xi,\eta){\rm d}_z\xi+\partial_{\eta}G(\xi,\eta){\rm d}_z\eta\\ &=&\partial_{\xi}G(\xi,\eta)+\partial_{\eta}G(\xi,\eta)\\ \partial_z^2\kappa(z,\zeta)&=&\partial_{\xi}^2G(\xi,\eta){\rm d}_z\xi+\partial_{\eta}\partial_{\xi}G(\xi,\eta){\rm d}_z\eta+\partial_{\xi}\partial_{\eta}G(\xi,\eta){\rm d}_z\xi+\partial_{\eta}^2G(\xi,\eta){\rm d}_z\eta\\ &=&\partial_{\xi}^2G(\xi,\eta)+2\partial_{\eta}\partial_{\xi}G(\xi,\eta)+\partial_{\eta}^2G(\xi,\eta)\\ \partial_{\zeta}\kappa(z,\zeta)&=&\partial_{\xi}G(\xi,\eta){\rm d}_{\zeta}\xi+\partial_{\eta}G(\xi,\eta){\rm d}_{\zeta}\eta\\ &=&\partial_{\xi}G(\xi,\eta)-\partial_{\eta}G(\xi,\eta)\\ \partial_{\zeta}^2\kappa(z,\zeta)&=&\partial_{\xi}^2G(\xi,\eta){\rm d}_{\zeta}\xi+\partial_{\eta}\partial_{\xi}G(\xi,\eta){\rm d}_{\zeta}\eta+\partial_{\xi}\partial_{\eta}G(\xi,\eta){\rm d}_{\zeta}\xi+\partial_{\eta}^2G(\xi,\eta){\rm d}_{\zeta}\eta\\ &=&\partial_{\xi}^2G(\xi,\eta)-2\partial_{\eta}\partial_{\xi}G(\xi,\eta)+\partial_{\eta}^2G(\xi,\eta)\\ \kappa(z,0)&=&G(\xi,\xi)=0\\ \kappa(z,z)&=&G(\xi,0)=-{\mu \over 4}\xi \end{eqnarray}$$

  于是我们得到坐标转换后的核方程：

$$\begin{eqnarray} \partial_{\eta}\partial_{\xi}G(\xi,\eta)&=&{\mu \over 4}G(\xi,\eta),\ (\xi,\eta)\in\tilde{\cal T}_R\tag{32}\\ G(\xi,\xi)&=&0\tag{33}\\ G(\xi,0)&=&-{\mu \over 4}\xi\tag{34} \end{eqnarray}$$

  现在我们开始求解该核方程。将式(32)在作用范围$\tilde{\cal T}_R$上积分：

$$\int_{\eta}^{\xi}\int_0^{\eta}\partial_{\eta'}\partial_{\xi'}G(\xi',\eta'){\rm d}\eta'{\rm d}\xi'={\mu \over 4}\int_{\eta}^{\xi}\int_0^{\eta}G(\xi',\eta'){\rm d}\eta'{\rm d}\xi'$$

  化简后得到：

$$G(\xi,\eta)=-{\mu \over 4}(\xi-\eta)+{\mu \over 4}\int_{\eta}^{\xi}\int_0^{\eta}G(\xi',\eta'){\rm d}\eta'{\rm d}\xi'\tag{35}$$

  在这里我们使用不动点迭代（Fixpunktiteration）求解式(35)中的$G(\xi,\eta)$。将式(35)右侧的第一项看作$G$的初始项$G_0$，第二项看作对$G$的方程$F[G]$：

$$\begin{eqnarray} G_0(\xi,\eta)&=&-{\mu \over 4}(\xi-\eta)\\ F[G] (\xi,\eta)&=&{\mu \over 4}\int_{\eta}^{\xi}\int_0^{\eta}G(\xi',\eta'){\rm d}\eta'{\rm d}\xi' \end{eqnarray}$$

  此时式(35)就化为了：

$$G(\xi,\eta)=G_0(\xi,\eta)+F[G] (\xi,\eta)\tag{36}$$

  使用如下等式对$G$进行迭代：

$$G_{i+1}(\xi,\eta)=G_0(\xi,\eta)+F[G_i] (\xi,\eta)\tag{37}$$

  一直迭代下去$G_i(\xi,\eta)$就会收敛为核方程$G(\xi,\eta)$：

$$\begin{eqnarray} G_1&=&G_0+F[G_0]\\ G_2&=&G_0+F[G_1]=G_0+F[G_0]+F^2[G_0]\\ &\vdots& \end{eqnarray}$$

  最终得到：

$$G=\lim_{i\to\infty}G_i=\sum_{i=0}^{\infty}F^i[G_0]\tag{38}$$

  设：

$$F^i[G_0]=\Delta G_i$$

  并且$\Delta G_i$满足：

$$\Delta G_{i+1}=F[\Delta G_i],\ \ \Delta G_0=G_0$$

  将$G_0$带入，经过一系列计算（这里我也没有算过，直接搬课件上的）得到：

$$\Delta G_i(\xi,\eta)=-\left({\mu \over 4}\right)^{i+1}{(\xi-\eta)\xi^i\eta^i \over i!(i+1)!},\ i\in{\Bbb N}\tag{39}$$

  带入式(38)得到：

$$G(\xi,\eta)=\sum_{i=0}^{\infty}\Delta G_i(\xi,\eta)=-{\mu \over 2}(\xi-\eta){I_1(\sqrt{\mu\xi\eta}) \over \sqrt{\mu\xi\eta}}\tag{40}$$

  其中$I_1(\cdot)$代表第一类贝塞尔函数。终于我们求得了$G(\xi,\eta)$的表达式，最后对其进行坐标变换我们就得到了最初的核函数$\kappa(z,\zeta)$：

$$\kappa(z,\zeta)=-\mu\zeta{I_1(\sqrt{\mu(z^2-\zeta^2)}) \over \sqrt{\mu(z^2-\zeta^2)}}\tag{41}$$

  将是(41)带入式(22)我们就求得了相应输入$u(t)$：

$$u(t)=-(\gamma+\mu_R)\int_0^1z{I_1(\sqrt{(\gamma+\mu_R)(1-z^2)}) \over \sqrt{(\gamma+\mu_R)(1-z^2)}}x(z,t){\rm d}z$$

  通过这个输入可以控制不稳定的原系统，将其转化为稳定的目标系统。在这里还需要注意的是，Backstepping求得的边界输入能够将系统所有特征值进行移动，因此它需要保证系统所有特征值都是能控的。

小结

1. 边界输入是作用在系统定义域边界的输入，因此它通过边界条件表示。
2. 边界输入的系统方程能够通过特殊方法转换为分布式输入的系统方程。
3. 使用Backstepping可以设计边界输入的反馈控制，但是计算相当繁琐。