机器学习中使用最多的算法莫过于神经网络与树形算法了,而树形算法的基础就是决策树(Decision Tree)。决策树是一种基本的分类与回归方法,相对于神经网络这种黑箱,决策树容易理解,并且运行速度快。但由于其结构较为简单,故预测能力有限,无法与强监督学习模型相提并论,需要进一步的优化。
概述
决策树的思想与我们在日常生活中进行判断或决策的过程类似。下面以判断“一个人对电脑游戏的喜爱程度”为例: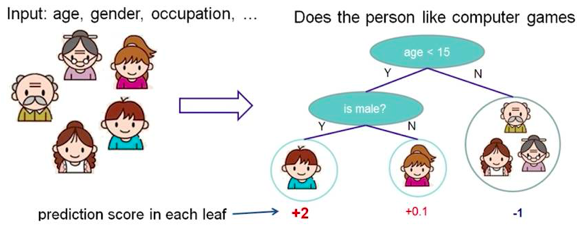
我们知道,一个人是否喜欢电脑游戏或对电脑游戏的喜爱程度可以通过他/她的年龄、性别、职业等特征来粗略估计。而这些特征的“重要性”是不同的,有些特征对我们判断的帮助更大,因此它们也就更加“重要”(在此例中,若我们发现年龄大的人不喜欢电脑游戏,不论男女和职业,那么年龄对于判断该问题更加“重要”)。在判断中我们会先考虑最“重要”的特征(年龄),再考虑第二“重要”的特征(性别),如此下去,最终得到输出(喜爱程度)。这就是一个最简单的决策树。
上面的例子中我们看出,决策树是一个倒置的树形结构。其中条件判断部分称为内部节点(internal node),决策输出部分称为叶节点(leaf)。虽然在实际中,数据集常常拥有很多特征,决策树也会变得非常庞大,但不可否认该算法使用时的简洁性。根据数据集的输出特性,决策树可以分为两类:分类决策树和回归决策树。分类决策树处理离散输出,而回归决策树处理连续输出。
不难发现,决策树最关键的部分就是各个中间节点。它们对特征取值进行,根据判断结果将样本归入其特定子分支中。中间节点根据判断特征属性分为三种情况:
1. 特征是离散值且不要求生成二叉树(即每个节点只能有两个分支)。此时将特征每个离散值作为一个分支。
2. 特征是离散值且要求生成二叉树。此时将离散值划分为两个子集,每个子集作为一个分支。
3. 特征是连续值。此时需要确定一个特征取值作为分裂点(split point),将特征根据取值大于或小于分裂点分为两种情况,每种情况作为一个分支。
此时决策树的构建就取决于两个核心问题:如何选择特征? 以及 如何选择划分点? 对此,我们有如下算法来解决这两个问题:ID3、C4.5与CART。
ID3
ID3(Iterative Dichotomiser 3)是一种构建分类决策树的算法。介绍它之前,我们首先要引入信息论中熵(entropy)的概念:熵表示状态的混乱程度,熵越大越混乱,状态的不确定性就越大。对ID3来说,数据集的熵越大,数据集就越“不纯”。若有数据集$D$,将它根据($m$个)离散输出进行划分,则$D$的熵表示为:
其中$p_i$表示分类$i$在整个数据集中的概率。若将$D$根据特征$A$划分为$v$个子数据集,每个子数据集的熵亦可由上式求出,则可以求得在经过特征$A$划分后,数据集$D$的期望熵为:
于是划分前后数据集$D$熵的下降值就是该划分的信息增益:
在分类问题中,我们希望划分后的子数据集越“纯”,也就是数据集$D$的熵最小,因此我们使用贪婪算法(greedy algorithn),选择信息增益最大的划分。每次划分都会使树长高一层,这样逐步下去,我们就构建了一棵决策树。下面以一个简单的例子来说明划分的选择过程:
| 日志数量 | 好友数量 | 是否使用真实头像 | 帐号是否真实 |
|---|---|---|---|
| 少 | 少 | 否 | 否 |
| 少 | 多 | 是 | 是 |
| 多 | 中 | 是 | 是 |
| 中 | 中 | 是 | 是 |
| 多 | 中 | 是 | 是 |
| 中 | 多 | 否 | 是 |
| 中 | 少 | 否 | 否 |
| 多 | 中 | 否 | 是 |
| 中 | 少 | 否 | 是 |
| 少 | 少 | 是 | 否 |
上表中的数据一共有三个特征:日志数量(L),好友数量(F)以及是否使用真实头像(H)。我们需要通过这三个特征来判断帐号是否真实。首先我们计算数据集的熵。数据集共有10个样本,其中7个是真的,3个是假的,因此数据集的熵为:
若根据日志数量进行划分,将样本划分为三个子数据集(多:$D_1$、中:$D_2$、少:$D_3$),则三个子数据集的熵分别为:
划分后的期望熵为:
根据日志数量划分的信息增益为:
同理可以得到$F$与$H$的信息增益分别为0.486与-0.034,因此我们选择好友数量作为第一次划分,以此类推就可以得到一棵决策树了。
C4.5
ID3有一个缺陷,就是它只考虑了子数据集的纯度,但忽略了特征本身的混乱程度。举个极端的情况,若前例数据集中每一个样本都有一个不同的账户ID,那么若以此为特征进行划分,就会将样本分为10个子数据集,每个子数据集只有一个样本,纯度最大。因此ID3会选择账户ID作为划分特征,但这是不可取的。
C4.5提供了一种解决方案,它考虑了特征的熵,并以此将信息增益标准化。特征的熵表示为:
标准化后的信息增益为:
之后就与ID3类似,选择信息增益标准化后最大的划分就可以了。接着之前的例子,我们可以将所得的信息增益标准化。特征$L$的熵为:
因此标准化后的信息增益为:
同理可以得到$F$与$H$标准化后的信息增益分别为0.319与-0.034,因此我们选择好友数量作为第一次划分,以此类推就可以得到一棵决策树了。
CART
CART(Classification And Regression Tree)是一种二叉决策树,可以对数据分类或者回归。与ID3、C4.5类似,CART也是通过选取最优划分来构建决策树的,但它使用的不是信息增益,而是划分的代价函数。
对于回归问题,代价函数表示为两个子数据集真实值与预测值的均方差之和:
其中预测值为每个子数据集输出的均值。若中间节点将数据集$D$划分为两个子数据集$D_1$、$D_2$,则$prediction_1$为$D_1$的均值,$prediction_2$为$D_2$的均值。
对于分类问题,我们使用Gini系数来表示一个数据集的混乱程度:
其中$p_i$为数据集中相同类别数据的比例。若数据集中只存在一个分类,是最好的情况,此时$G=0$。最糟糕的情况就是数据集中所有类别都有相同的比例,此时$G=1-p_i$。
分类问题的代价函数表示为两个子数据集Gini系数的期望:
无论回归还是分类问题,当构建决策树时,算法会考虑每个特征,计算它们的代价函数,并选取最小代价的特征及划分点,以此下去即可。
优化
若数据的特征很多,决策树的构建过程就会一直进行下去,这样会产生过拟合问题,因此在实际操作中我们需要指定停止条件,并可以适当对枝叶进行修剪,除此之外还可以使用集成树模型来进一步提升预测效果。
设置停止条件
通常设置的停止条件有如下几种:
1. 叶节点中只有一种类型时停止:这是最直观的方式,仅限于分类问题,并容易导致过拟合。
2. 设置叶节点的最小样本数量:若训练过程中,数据集到达叶节点的样本数量过小,那么我们就舍去这个叶节点。
3. 设置树的最大深度:即限制样本到达叶节点时所通过的中间节点数量。
修剪
对决策树进行修剪可以进一步提高其分类表现。修剪过程中,在不影响准确度的情况下,我们可以将不重要的枝叶移除。这样可以降低决策树的复杂度,并减少过拟合问题。
集成树模型
单棵决策树稳定性通常较低且方差较高,难以达到很好的效果。使用集成学习可以降低降低决策树的方差,从而提高整体的预测能力。常见的集成树模型有随机森林、GBM(Gradient boosting machine)与xgboost。
随机森林(Random Forest)采用多个决策树的投票机制来改善决策树的预测能力。训练过程中,我们每次都随机取部分训练样本来训练决策树,一直重复,我们就能训练出许多不同的决策树,它们形成了一个森林。之后使用这个森林对未知数据进行预测。每个决策树可能会预测出不同的结果,将这些结果汇总并选取投票最多的分类作为预测值。实践证明,随机森林的运行效率和准确率较高,实现起来也较为简单,相较普通决策树更为常用。
GBM与xgboost我还没有研究,在此先省略。
小结
- 决策树通过选取特征及划分点来对数据进行划分。
- 构建决策树的算法有:ID3、C4.5与CART,其中ID3与C4.5仅用于分类问题,CART能够用于分类或回归问题。
- 决策树容易过拟合,需要进行优化。