计算机视觉（一）：图像表示与梯度

  计算机视觉，顾名思义就是使计算机能够像人眼一样“看”东西的科学。一张图片，人可以将它抽象并快速提取其中的有效信息。而对于计算机来说，图片就是一个特殊的矩阵，需要通过一系列算法来得到相关信息。本次学习材料主要是TUM Computer Vision课堂内容以及一些相关论文。

图像表示

  首先介绍一下图像的基本知识。图像一般可分为彩色图和灰度图：彩色图每个点的颜色可以通过RGB三种颜色混合而成，因此彩色图通常有RGB三个通道；而灰度图每个点只有一个灰度值。

  彩色图可以将三个通道合并，转化为灰度图，其公式如下：

$$I=0.299R+0.587G+0.114B$$

  在现实中，人眼看到的东西都是连续的，但在计算机中我们需要将其离散化，并赋予每个点坐标与数值。其示意图如下：

  图像在计算机中的坐标原点为图像左上角，其$x,y$轴与通常坐标系不同，在将来的操作中需要格外注意。这里我们将图像的矩阵表示为$I$，而图中某点的数值表示为$I(x,y)$，其取值范围通常为$[0,1]$或$[0,255]$。在之后的讨论中，我们默认对灰度图进行操作。

梯度计算

  梯度在连续函数中可以通过求导计算，但在离散函数中只能通过一些方法来近似。其中最直接的方法就是将离散点与相邻点的差值作为该点梯度：

$$\nabla I(x,y)=\begin{bmatrix}{ {\Bbb d} \over {\Bbb d}x}I(x,y) \\ { {\Bbb d} \over {\Bbb d}y}I(x,y) \end{bmatrix} = \begin{bmatrix}I(x+1,y)-I(x,y) \\ I(x,y+1)-I(x,y)\end{bmatrix}$$

  这种方法虽然简单，但误差较大。在实际中，我们计算梯度的思路是：先将离散函数通过辅助函数连续化，再对连续化后的函数进行求导得到梯度。
  其中连续化是将连续的辅助函数与离散函数卷积，得到一个重构的连续函数。在这里我们以一维数据为例，其中连续函数用$f(x)$表示，离散函数用$f[x]$表示：

$$f(x)\approx\sum_{k=-\infty}^{\infty}f[k]h(x-k)=f[x]\ast h(x)$$

  对$f(x)$求导便可以得到函数的梯度：

$$f'(x)\approx{ {\Bbb d} \over {\Bbb d}x}(f[x]\ast h(x))=\sum_{k=-\infty}^{\infty}f[k]h'(x-k)=f[x]\ast h'(x)$$

  则图像上每一点的梯度为：

$$f'[x]=f[x]\ast h'[x]=\sum_{k=-\infty}^{\infty}f[x-k]h'[k]$$

  实际中我们无法做无穷次的累加，因此采用近似的方式得到函数及其导数：

$$\begin{split} f[x]&=\sum_{k=-n}^{n}f[x-k]h[k]\\ f'[x]&=\sum_{k=-n}^{n}f[x-k]h'[k] \end{split}$$

  其中辅助函数$h(x)$我们可以选择高斯函数或Sinc函数。

高斯函数

  高斯函数一般表达式如下：

$$g(x)=Ce^{-x^2 \over 2\sigma^2}$$

  其图像及导数图像如下：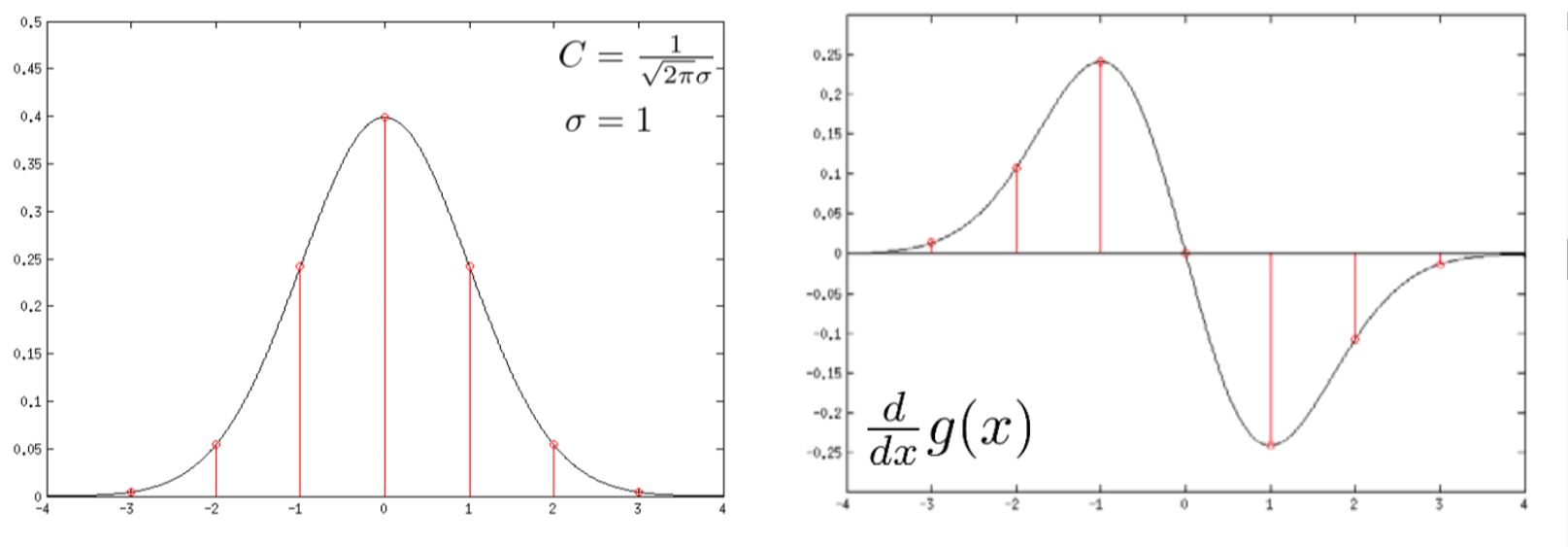

  图中红线表示相邻采样点的取值。可以发现，高斯函数会对相邻采样点取值有影响，从而产生一些偏差。

Sinc函数

  Sinc函数表达式如下：

$$h(x)={\rm sinc}(x)={\sin(\pi x) \over \pi x}, {\rm sinc}(0)=1$$

  其图像及其导数图像如下：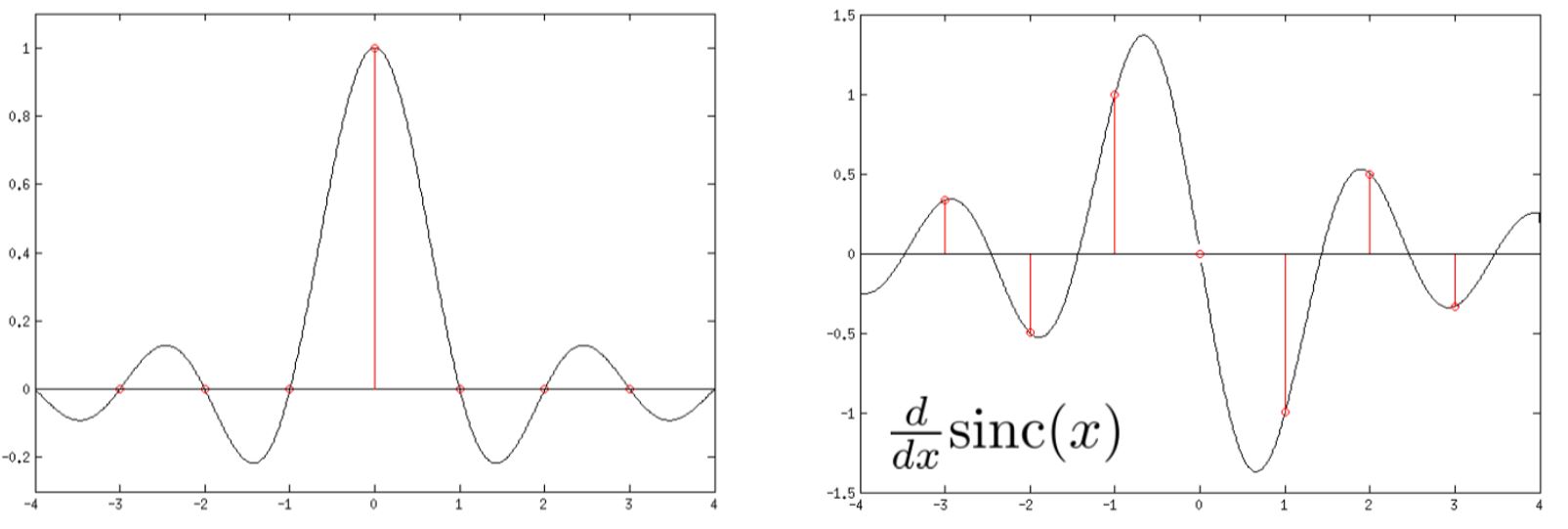

  从图中可以发现，Sinc函数在相邻采样点取值均为0，克服了高斯函数的缺陷。但其导数图像衰弱程度比高斯函数慢很多。
  因此通常我们在连续化原函数时使用Sinc函数，在计算梯度时使用高斯函数。

Sobel滤波器

  将上述一维的数据拓展为二维，使用高斯函数作为辅助函数，我们得到：

$$\begin{split} &I(x,y)\approx I[x,y]\ast h(x,y)=\sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}I[x.y]g(x-k)g(y-l)\\ &{ {\rm d} \over {\rm d}x}I(x,y) \approx I[x,y]\ast { {\rm d} \over {\rm d}x}h(x,y)=\sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}I[x.y]g'(x-k)g(y-l)\\ &{ {\rm d} \over {\rm d}y}I(x,y) \approx I[x,y]\ast { {\rm d} \over {\rm d}y}h(x,y)=\sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}I[x.y]g(x-k)g'(y-l) \end{split}$$

  则图像上每一点的梯度为:

$$\begin{split} &{ {\rm d} \over {\rm d}x}I[x,y]=\sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}I[x.y]g'[x-k]g[y-l]=\sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}I[x-k.y-l]g'[k]g[l]\\ &{ {\rm d} \over {\rm d}y}I[x,y]=\sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}I[x.y]g[x-k]g'[y-l]=\sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}I[x-k.y-l]g[k]g'[l] \end{split}$$

  近似后得到：

$$\begin{split} { {\rm d} \over {\rm d}x}I[x,y]=\sum_{k=-1}^{1}\sum_{l=-1}^{1}I[x-k.y-l]g'[k]g[l]\\ { {\rm d} \over {\rm d}y}I[x,y]=\sum_{k=-1}^{1}\sum_{l=-1}^{1}I[x-k.y-l]g[k]g'[l] \end{split}$$

  上式可以发现，图像中点的梯度就相当于其相邻像素点取值分别乘以相应权重再相加，因此可以将这些权重表示为一个矩阵。为了使权重相加为1，我们取：

$$C=(1+2e^{-{1 \over 2\sigma^2 } })^{-1}$$

  当$\sigma=\sqrt{1 \over 2\log2}$时：

$$\begin{split} &g'[k]g[l]\Rightarrow {1 \over 8}\log2\begin{bmatrix}+1 & \ \ 0\ & -1\\+2 & \ \ 0\ & -2\\+1 & \ \ 0\ & -1\end{bmatrix}\\ &g[k]g'[l]\Rightarrow {1 \over 8}\log2\begin{bmatrix}+1 & +2 & +1\\0 & 0 & 0\\-1 & -2 & -1\end{bmatrix} \end{split}$$

  为了方便计算，我们将上式整数化，得到横向与纵向Sobel滤波器分别为：

$$\begin{split} 横向{\rm Sobel}滤波器：\begin{bmatrix}+1 & \ \ 0\ & -1\\+2 & \ \ 0\ & -2\\+1 & \ \ 0\ & -1\end{bmatrix}\\ 纵向{\rm Sobel}滤波器：\begin{bmatrix}+1 & +2 & +1\\0 & 0 & 0\\-1 & -2 & -1\end{bmatrix} \end{split}$$

  在实际应用中我们只需要将图像矩阵与Sobel滤波器卷积就可以得到图像的梯度矩阵了。

小结

1. 图像在计算机中表示为矩阵形式。
2. 图像梯度通过Sobel滤波器估计：横向滤波器计算$x$轴方向导数；纵向滤波器计算$y$轴方向导数。